Bio
Welcome to my homepage! Professor Bouzebda received his Ph.D. in Statistics from Pierre and Marie Curie University (Paris VI) in 2007. His research interests lie at the intersection of theoretical and applied statistics, encompassing a diverse range of topics including censored data, functional data analysis, multivariate methods, extreme value theory, bootstrap techniques, and the application of artificial intelligence algorithms to high-dimensional and large-scale data.
Professor Bouzebda is the author of more than 170 peer-reviewed articles published in leading international journals, attesting to the breadth and impact of his scholarly contributions. His work is characterized by methodological rigor and a strong commitment to advancing statistical science across disciplinary boundaries.
He has served, and continues to serve, as an Associate Editor for several prominent statistical journals, including Dependence Modeling and Communications in Statistics. He currently holds the rank of Full Professor of Mathematical Statistics and serves as Director of the Research Laboratory in Applied Mathematics (LMAC) at the Université de Technologie de Compiègne, France.
Academic Positions
-
2016 Present
Full Professor
Laboratory LMAC
Department Computer Science
University of Technology of Compiègne
-
2011 2016
Assistant Professor
Laboratory LMAC
Department Computer Science
University of Technology of Compiègne
Education
-
HDR 2016
Habilitation à Diriger des Recherches in Mathematics
Research Laboratory in Applied Mathematics
Univeristy of Technology of Compiègne
-
Ph.D. Student 2007
Ph.D. in Mathematics
Departement of Statistics LSTA
University Pierre and Marie Curie (now Sorbonne Univ.)
Salim Bouzebda
CV
HDR in mathematics (2016)
- Université de Technologie de Compiègne
- Title: Contribution à l’inférence statistique non-paramétrique et semi-paramétrique : pro- cessus empirique, bootstrap et copules
Ph.D. in mathematics (2007)
- University Pierre and Marie Curie
- Title: Contribution à l’Étude des Statistiques des Extrêmes et aux Tests d’Indépendance
Teaching
Engaging with students is a fundamental aspect of any academic career. Throughout my teaching experience at various universities, I have taught mathematics, statistics, and machine learning at all levels, to both specialists in the field and students from other disciplines.
University of Technology of Compiègne
-
2021--AI28 - Machine Learning (M. Alaya)Machine learning (apprentissage automatique ou apprentissage machine) est une branche de l’intelligence artificielle (IA), qui est elle même une branche de la science de données. Ce cours est conçu pour faire une présentation des méthodologies et algorithmes de machine learning, dans leurs concepts comme dans leurs cas typiques d’applications. La mise en ouvre de ces concepts se fait en langage de programmation Python.
Partie 1: Introduction générale au machine learrning et prise en main de Python
Partie 2 : Formalisme mathématique d’un problème de machine learning
Partie 3 : Apprentissage supervisé
Partie 4 : Apprentissage non-supervisé
-
2025Applied Machine Learning for Process Engineering (M. Alaya)Machine learning appliqué pour le génies des procédés.
1. Introduction générale au machine learning
2. Librairie Python : Pandas, Scipy, Matplotlib, Pyplot, Seaborn
3. Régression linéaire multiple, Régression pénalisée, SVM, Arbres de décision, Forêts aléatoires
4. Réduction de la dimension, Analyse en composantes principales (ACP), Clustering
5. Applications sur des données chimiques réelles
-
2011--MT11 - Real Analysis and AlgebraSynthèse des mathématiques du premier cycle: fonctions d’une ou plusieurs variables, courbes et surfaces, intégrales simples et multiples, équations différentielles, bases de l’algèbre linéaire. L’enseignement se présente sous forme d’un cours-TD fondé sur un document intégrant cours et exercices.
-
2015--MT22 - Multivariate CalculusContinuité, différentiabilité des fonctions de plusieurs variables réelles. Analyse vectorielle. Courbes et surfaces de \(\mathbb{R}^3\). Intégrales multiples ; curvilignes, surfaciques. Théorèmes intégraux.
-
2012--SY01 - ProbabilityNotion d’aléatoire et introduction au calcul des probabilités.
Research Summary
My research lies at the intersection of mathematical statistics, statistical machine learning theory and its modern applications, with a strong emphasis on both methodological development and theoretical foundations.
Research Interests
- Statistical Machine Learning Theory & Applications
- Machine Learning (ML) and Deep Learning (DL)
- High-dimensional Statistics
- Empirical process theory
- U-Empirical process
- Bootstrap
- Semi/Nonparametric statistical theory
- Functional data analysis
- Multivariate analysis : Copula
- Change point analysis
- Limit theorems for dependent random variables
- Statistics for stochastic processes
- Data Science
Interdisciplinary Project: Artificial Intelligence for Mecanic (AI4Meca)
-
2024-2025Unsupervised Deep Clustering of combined data from multi-Structural Health Monitoring Techniques obtained on Smart Polymer-Matrix Composites embedded with Piezoelectric Transducers
This project is a first collaboration with Matériaux et Surfaces team of Roberval Laboratory in UTC. It concerns data fusion and clustering methods utilizing deep neural networks (DNN) to classify heterogeneous data from different acquisition methods. A machine learning algorithm, specifically a convolutional autoencoder, was evaluated by clustering datasets obtained from load-unload tensile tests of smart specimens embedding PZTs and PVDF transducers. These piezoelectric transducers were employed to collect multi-source data for SHM purposes. Additionally, external equipment such as DIC and AE were used for both validation and the initial testing of the DNN configuration. The project highlights the feasibility of using DNN architecture to classify multi-acquired and merged data for SHM. -
2025-2028Generative Deep Learning for Atomistically Engineered Materials: Synergistic Integration of Molecular Dynamics Simulations, Experiments and Data Augmentation
This project is a second collaboration with Matériaux et Surfaces team of Roberval Laboratory in UTC. The primary objective of the project is to advance the development of nanostructured materials with tailored properties through novel approaches. It proposes an integrated, data-driven approach to expedite the development of advanced nanostructured materials. Using machine learning-driven data augmentation—specifically GANs, VAEs, and hybrid architectures—we address the constraints of limited datasets in materials science. This strategy complements existing experimental and atomistic modeling efforts, allowing robust predictions of material behavior across scales. It reduces time and cost associated with iterative experimentation and simulation. Moving forward, deeper validation of the synthetic data’s physical relevance—via experiments and atomistic simulations—will be crucial.
Interdisciplinary Project: Artificial Intelligence for Chemical (AI4Chem)
-
2025-2026Machine Learning Prediction Modelling for Chemistry with emphasis on High-Through Experiment
This project is a collaboration with the team Activités Microbiennes et Bioprocédés (MAB) of TIMR Laboratory U High-throughput experimentation in chemistry enables rapid and automated exploration of chem- ical space, facilitating the discovery of new drugs. Integrating machine learning techniques with these high-throughput methods can further accelerate and enhance the exploration and optimization of chemical space.
Selected recent papers
The full list of publications is available on the LMAC UTC website .
Filter by type:
Sort by year:
Bounds in Wasserstein Distance for Locally Stationary Functional Time Series
PreprintarXiv, 2025
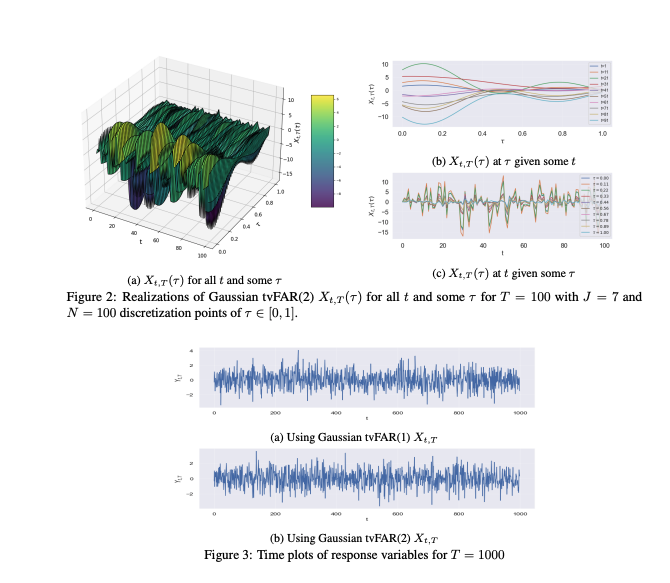
Abstract
Functional time series (FTS) extend traditional methodologies to accommodate data observed as functions/curves. A significant challenge in FTS consists of accurately capturing the time-dependence structure, especially with the presence of time-varying covariates. When analyzing time series with time-varying statistical properties, locally stationary time series (LSTS) provide a robust framework that allows smooth changes in mean and variance over time. This work investigates Nadaraya-Watson (NW) estimation procedure for the conditional distribution of locally stationary functional time series (LSFTS), where the covariates reside in a semi-metric space endowed with a semi-metric. Under small ball probability and mixing condition, we establish convergence rates of NW estimator for LSFTS with respect to Wasserstein distance. The finite-sample performances of the model and the estimation method are illustrated through extensive numerical experiments both on functional simulated and real data.
Bounds in Wasserstein Distance for Locally Stationary Processes
Preprint
arXiv, 2024
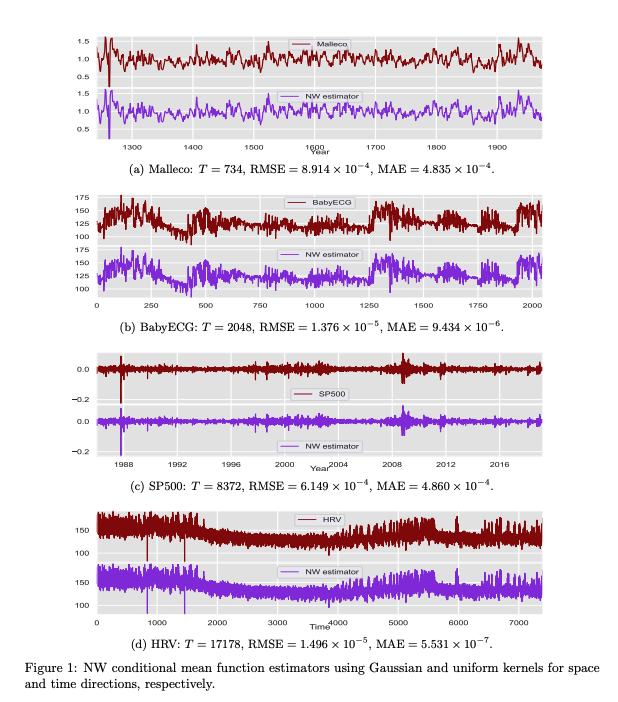
Abstract
Locally stationary processes (LSPs) provide a robust framework for modeling time-varying phenomena, allowing for smooth variations in statistical properties such as mean and variance over time. In this paper, we address the estimation of the conditional probability distribution of LSPs using Nadaraya-Watson (NW) type estimators. The NW estimator approximates the conditional distribution of a target variable given covariates through kernel smoothing techniques. We establish the convergence rate of the NW conditional probability estimator for LSPs in the univariate setting under the Wasserstein distance and extend this analysis to the multivariate case using the sliced Wasserstein distance. Theoretical results are supported by numerical experiments on both synthetic and real-world datasets, demonstrating the practical usefulness of the proposed estimators.
Sparsified-Learning for Heavy-Tailed Locally Stationary
Preprint
arXiv, 2025
Abstract
Sparsified Learning is ubiquitous in many machine learning tasks. It aims to regularize the objective function by adding a penalization term that considers the constraints made on the learned parameters. This paper considers the problem of learning heavy-tailed LSP. We develop a flexible and robust sparse learning framework capable of handling heavy-tailed data with locally stationary behavior and propose concentration inequalities. We further provide non-asymptotic oracle inequalities for different types of sparsity, including ℓ1-norm and total variation penalization for the least square loss.
A nonparametric distribution-free test of independence among continuous random vectors based on \(L_1\)-norm
Journal
Bernoulli, 2025
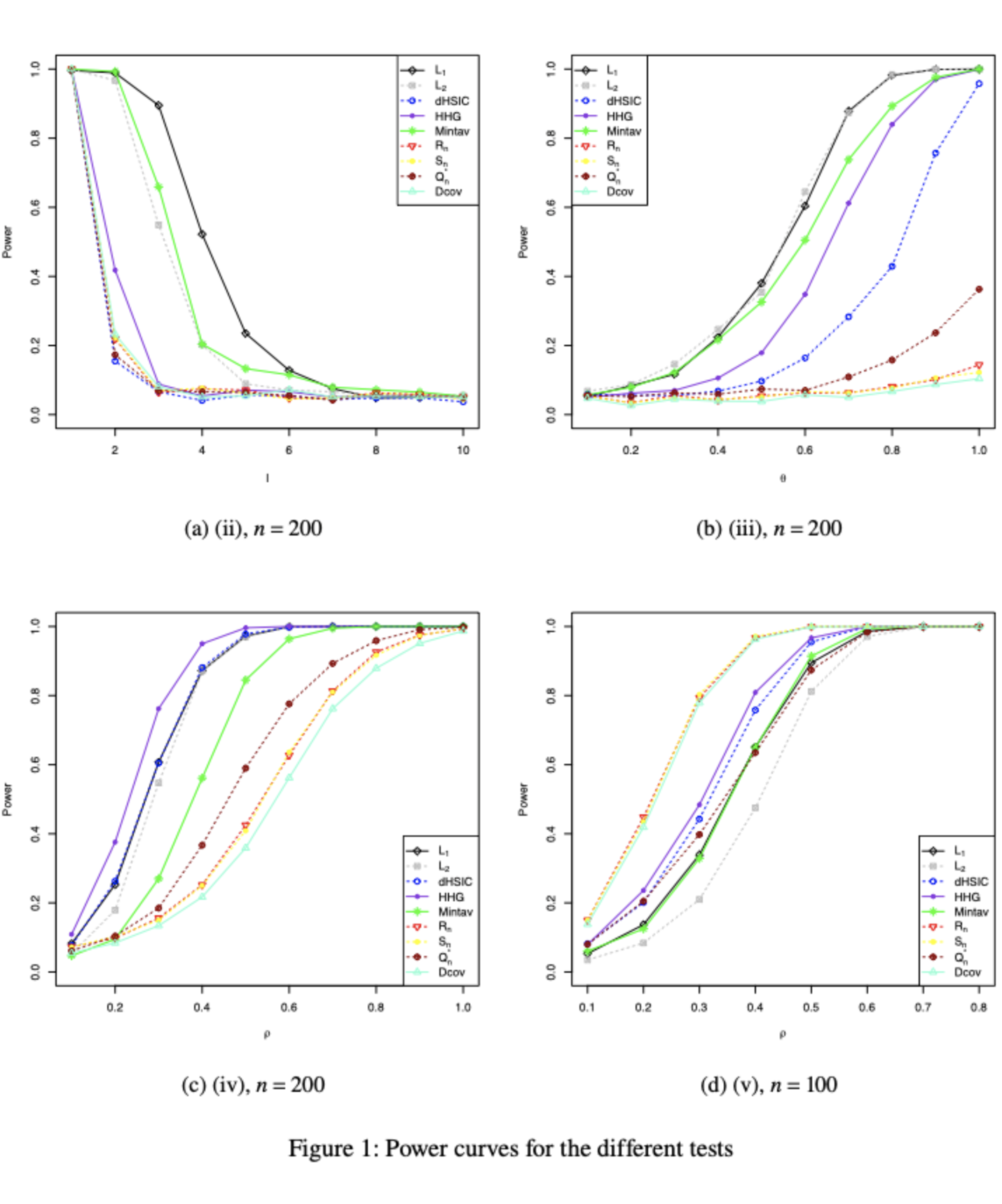
Abstract
We propose a novel statistical test to assess the mutual independence of multidimensional random vectors. Our approach is based on the \(L_1\)-distance between the joint density function and the product of the marginal densities associated with the presumed independent vectors. Under the null hypothesis, we employ Poissonization techniques to establish the asymptotic normal approximation of the corresponding test statistic, without imposing any regularity assumptions on the underlying Lebesgue density function, denoted as \(f(\cdot)\). Remarkably, we observe that the limiting distribution of the \(L_1\)-based statistics remains unaffected by the specific form of \(f(\cdot)\). This unexpected result contributes to the robustness and versatility of our method. Moreover, our tests exhibit nontrivial local power against a subset of local alternatives, which converge to the null hypothesis at a rate of \({n{ n^{\tiny -1/2}h_n^{\tiny -{d/4}}}}\), \(d\geq 2\), where \(n\) represents the sample size and \(h_n\) denotes the bandwidth. Finally, the theory is supported by a comprehensive simulation study to investigate the finite-sample performance of our proposed test. The results demonstrate that our testing procedure generally outperforms existing approaches across various examined scenarios.
Nonparametric conditional \(U\)-statistics on Lie groups with measurement errors
Journal
Journal of Complexity, 2025
Abstract
This study presents a comprehensive framework for conditional U-statistics of a general order in the context of Lie group-valued predictors affected by measurement errors. Such situations arise in a variety of modern statistical problems. Our approach is grounded in an abstract harmonic analysis on Lie groups, a setting relatively underexplored in statistical research. In a unified study, we introduce an innovative deconvolution method for conditional U-statistics and investigate its convergence rate and asymptotic distribution for the first time. Furthermore, we explore the application of conditional U-statistics to variables that combine, in a nontrivial way, Euclidean and non-Euclidean elements subject to measurement errors, an area largely uncharted in statistical research. We derive general asymptotic properties, including convergence rates across various modes and the asymptotic distribution. All results are established under fairly general conditions on the underlying models. Additionally, our results are used to derive the asymptotic confidence intervals derived from the asymptotic distribution of the estimator. We also discuss applications of the general approximation results and give new insights into the Kendall rank correlation coefficient and discrimination problems.
Limit theorems for nonparametric conditional \(U\)-statistics smoothed by asymmetric kernels.
Journal
AIMS Mathematics, 2024
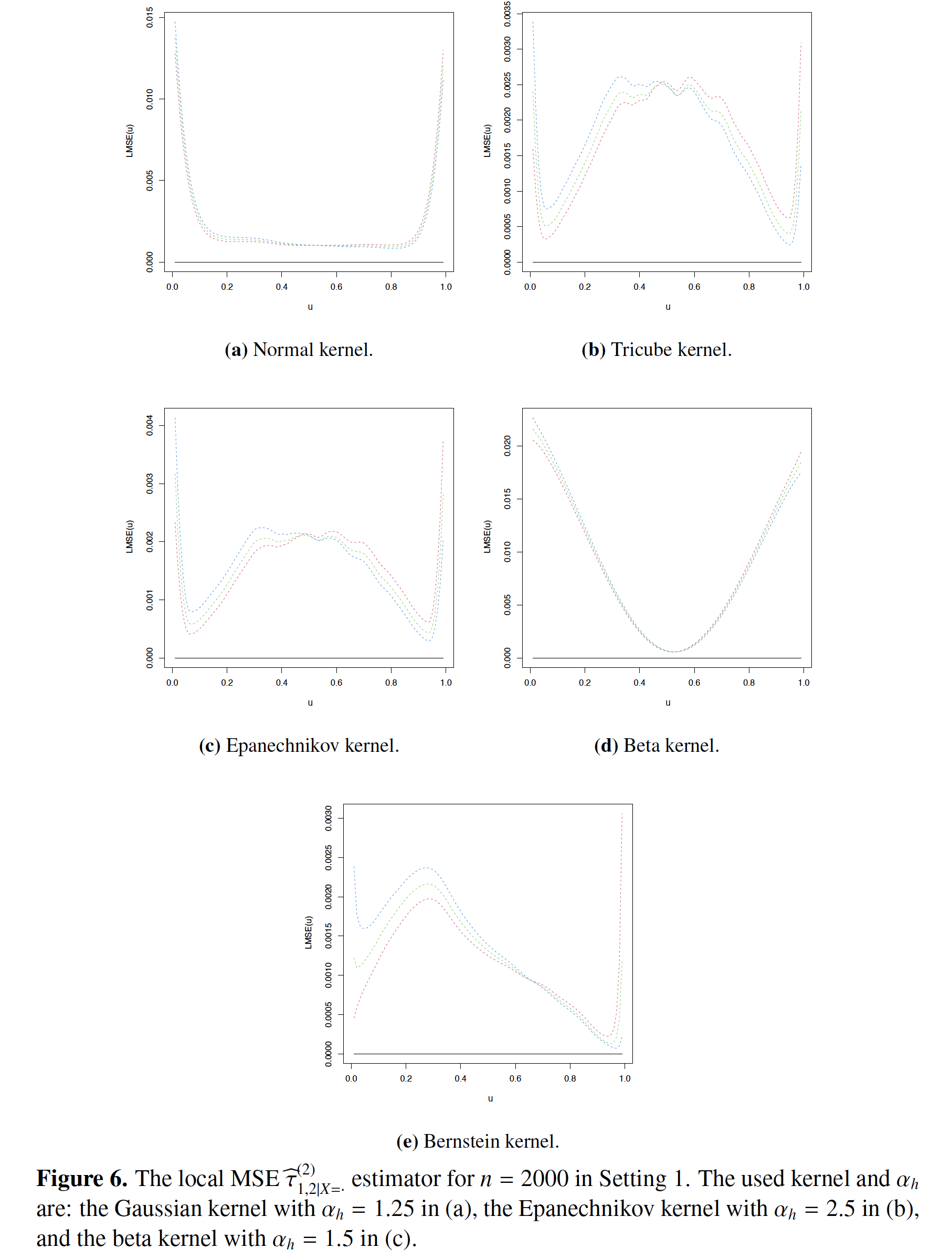
Abstract
\(U\)-statistics represent a fundamental class of statistics used to model quantities derived from responses of multiple subjects. These statistics extend the concept of the empirical mean of a \(d\)-variate random variable X by considering sums over all distinct \(m\)-tuples of observations of X. Within this realm, W. Stute introduced conditional \(U\)-statistics, a generalization of the Nadaraya-Watson estimators for regression functions, and demonstrated their strong point-wise consistency. This paper presented a first theoretical examination of the Dirichlet kernel estimator for conditional \(U\)-statistics on the \(dm\)-dimensional simplex. This estimator, being an extension of the univariate beta kernel estimator, effectively addressed boundary biases. Our analysis established its asymptotic normality and uniform strong consistency. Additionally, we introduced a beta kernel estimator specifically tailored for conditional \(U\)-statistics, demonstrating both weak and strong uniform convergence. Our investigation considered the expansion of compact sets and various sequences of smoothing parameters. For the first time, we examined conditional \(U\)-statistics based on mixed categorical and continuous regressors. We presented new findings on conditional U-statistics smoothed by multivariate Bernstein kernels, previously unexplored in the literature. These results are derived under sufficiently broad conditions on the underlying distributions. The main ingredients used in our proof were truncation methods and sharp exponential inequalities tailored to the \(U\)-statistics in connection with the empirical processes theory. Our theoretical advancements significantly contributed to the field of asymmetric kernel estimation, with potential applications in areas such as discrimination problems, \(\ell\)-sample conditional \(U\)-statistics, and the Kendall rank correlation coefficient. Finally, we conducted some simulations to demonstrate the small sample performances of the estimators.
Oracle inequalities and upper bounds for kernel conditional estimators \(U\)-statistics estimators on manifolds and more general metric spaces associated with operators.
Journal
Stochastics, 2024
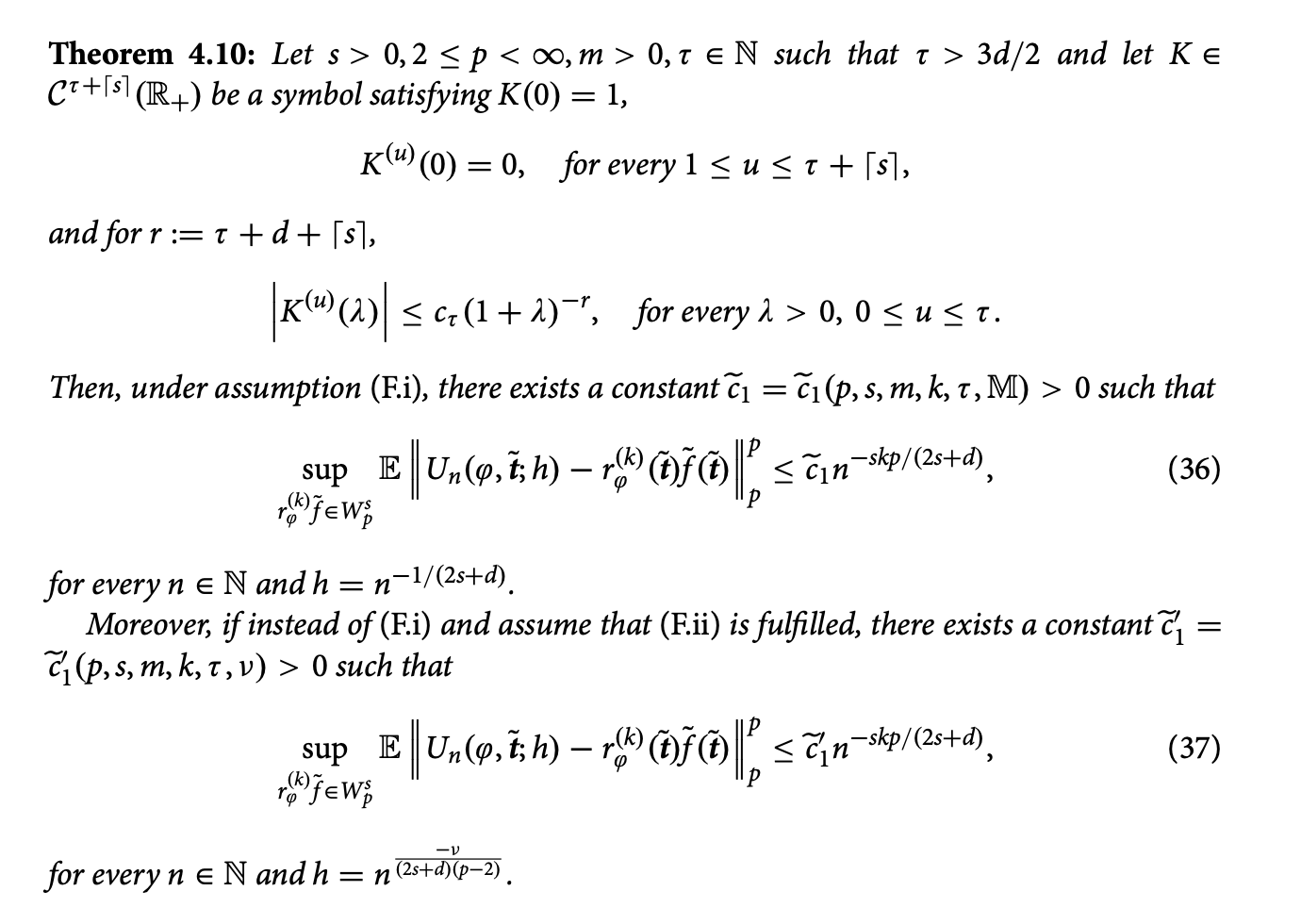
Abstract
\(U\)-statistics represent a fundamental class of statistics that emerge from modelling quantities of interest defined by multi-subject responses. These statistics generalize the empirical mean of a random variable \(\mathbf{X}\) to summations encompassing all distinct \(k\)-tuples of observations drawn from \(\mathbf{X}\). A significant advancement was made by Stute [Conditional \(U\)-statistics. Ann. Probab. 19 (1991), pp. 812-825] [MR1106287], who introduced conditional \(U\)-statistics as a generalization of the Nadaraya-Watson estimates for regression functions. Stute demonstrated their robust pointwise consistency towards the conditional function \[ r^{(k)}(\varphi, \tilde{\mathbf{t}})=\mathbb{E}\left(\varphi\left(\mathbf{Y}_1, \ldots, \mathbf{Y}_k\right) \mid\left(\mathbf{X}_1, \ldots, \mathbf{X}_k\right)=\tilde{\mathbf{t}}\right), \quad \text { for } \tilde{\mathbf{t}} \in \mathbb{R}^{p k} ,\] where $\phi$ is a measurable function. In this investigation, we develop oracle inequalities and upper bounds for kernel-based estimators of conditional $U$-statistics of general order, applicable across a wide range of metric spaces associated with operators. Our analysis specifically targets doubling measure metric spaces, incorporating a non-negative self-adjoint operator characterized by Gaussian regularity in its heat kernel. Remarkably, our study achieves an optimal convergence rate in certain cases. To derive these results, we explore the regression function within a general framework, introducing several novel insights. These findings are established under sufficiently broad conditions on the underlying distributions. The theoretical results serve as essential tools for advancing the field of general-valued data, with potential applications including the examination of conditional distribution functions, relative-error prediction, the Kendall rank correlation coefficient, and discrimination problems—areas of significant independent interest.
Empirical likelihood based confidence regions for functional of copulas.
Journal
Journal of Nonparametric Statistics, 2024
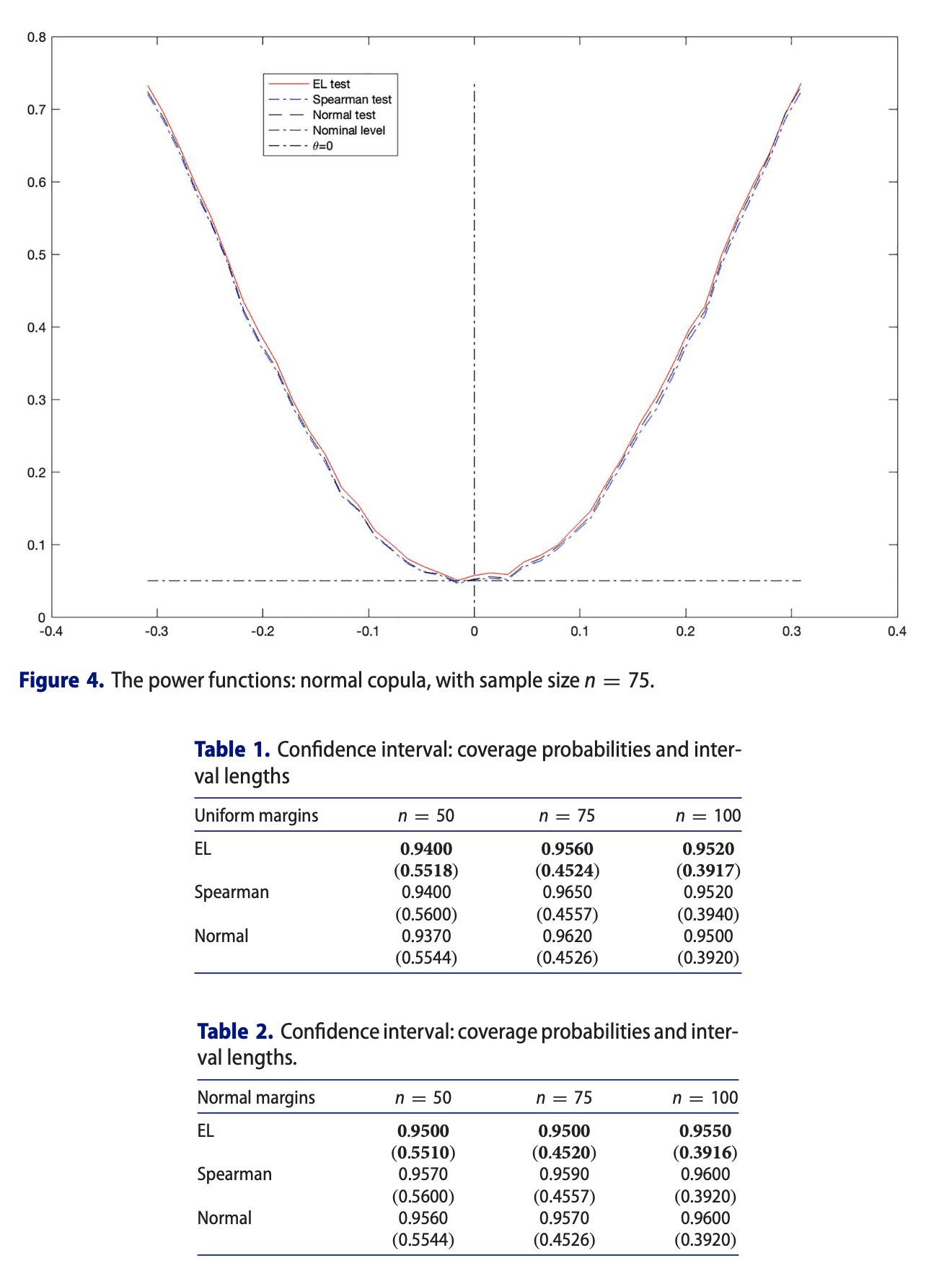
Abstract
In the present paper, we are mainly concerned with the statistical inference for the functional of nonparametric copula models satisfying linear constraints. The asymptotic properties of the obtained estimates and test statistics are given. Finally, a general notion of bootstrap for the proposed estimates and test statistics, constructed by exchangeably weighting sample, is presented, which is of its own interest. These results are proved under some standard structural conditions on some classes of functions and some mild conditions on the model, without assuming anything about the marginal distribution functions, except continuity. Our theoretical results and numerical examples by simulations demonstrate the merits of the proposed techniques.
Renewal type bootstrap for increasing degree \(U\)-process of a Markov chain.
Journal
Journal of Multivariate Analysis, 2023
Abstract
In this paper, we investigate the uniform limit theory for a \(U\)-statistic of increasing degree, also called an infinite-degree \(U\)-statistic. Infinite-degree \(U\)-statistics (IDUS) (or infinite-order \(U\)-statistics (IOUS)) are useful tool for constructing simultaneous prediction intervals that quantify the uncertainty of several methods such as subbagging and random forests. The stochastic process based on collections of \(U\)-statistics is referred to as a \(U\)-process, and if the \(U\)-statistic is of infinite-degree, we have an infinite-degree \(U\)-process. Heilig and Nolan (2001) provided conditions for the pointwise asymptotic theory for the infinite-degree \(U\)-processes. The main purpose here is to extend their findings to the Markovian setting. The second aim is to provide the uniform limit theory for the renewal bootstrap for the infinite-degree \(U\)-process, which is of its own interest. The main ingredients are the decoupling technique combined with symmetrization techniques of Heilig and Nolan (2001) to obtain uniform weak law of large numbers and functional central limit theorem for the infinite-degree U-process. The results obtained in this paper are, to our knowledge, the first known results on the infinite-degree \(U\)-process in the Markovian setting.
Asymptotic properties of semiparametric \(M\)--estimators with multiple change points.
Journal
Physica A: Statistical Mechanics and its Applications, 2023
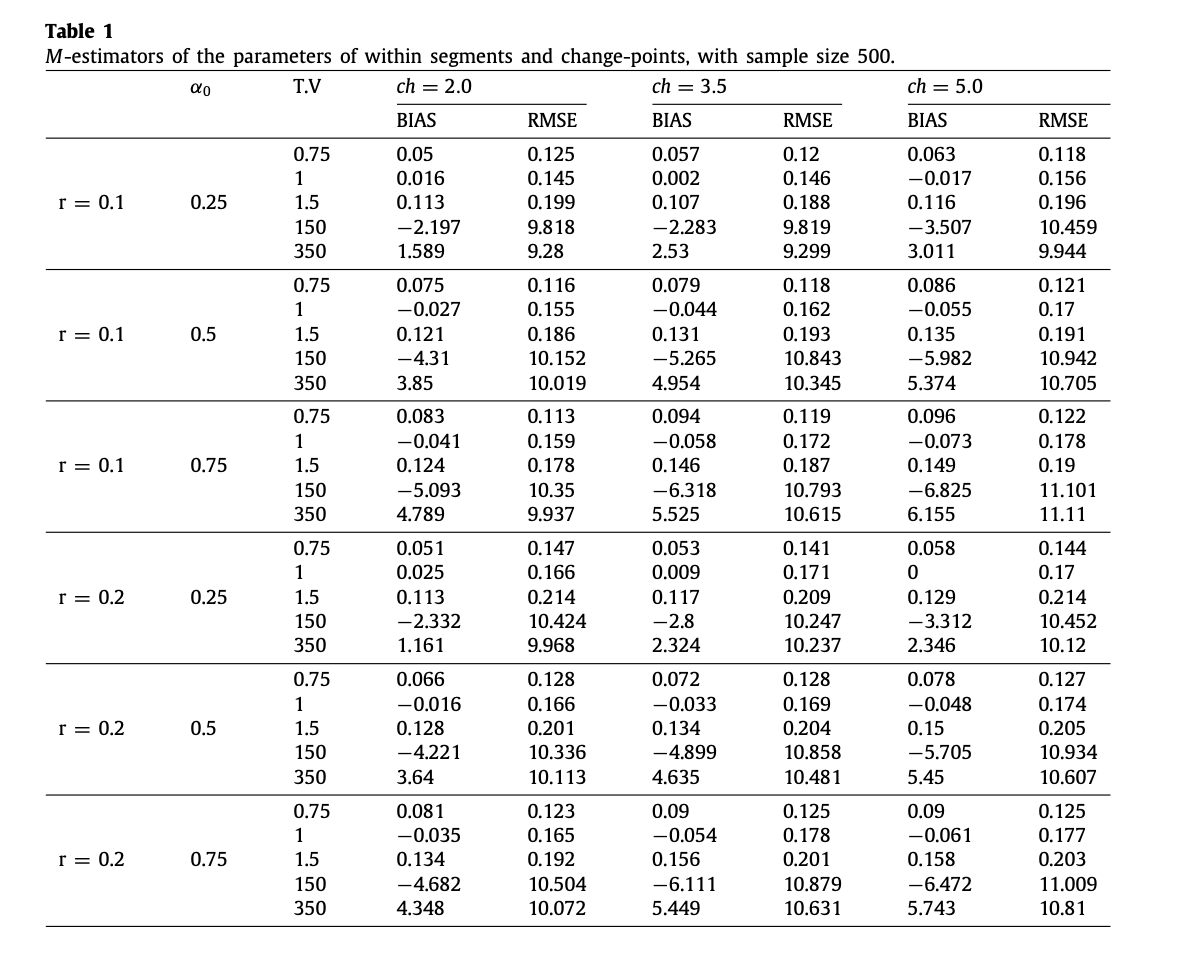
Abstract
Statistical models with multiple change points are used in many fields; however, the theoretical properties of semiparametric \(M\)-estimators of such models have received relatively little attention. The main purpose of the present work is to investigate the asymptotic properties of semiparametric \(M\)-estimators with non-smooth criterion functions of the parameters of a multiple change-point model for a general class of models in which the form of the distribution can change from segment to segment and in which, possibly, there are parameters that are common to all segments. Consistency of the semiparametric \(M\)-estimators of the change points is established and the rate of convergence is determined. The asymptotic normality of the semiparametric \(M\)-estimators of the parameters of the within-segment distributions is established under quite general conditions. These results, together with a generic paradigm for studying semiparametric \(M\)-estimators with multiple change points, provide a valuable extension to previous related research on (semi)parametric maximum-likelihood estimators. For illustration, the classification with missing data in the model is investigated in detail and a short simulation result is provided.
The consistency and asymptotic normality of the kernel type expectile regression estimator for functional data.
Journal
Journal of Multivariate Analysis, 2021
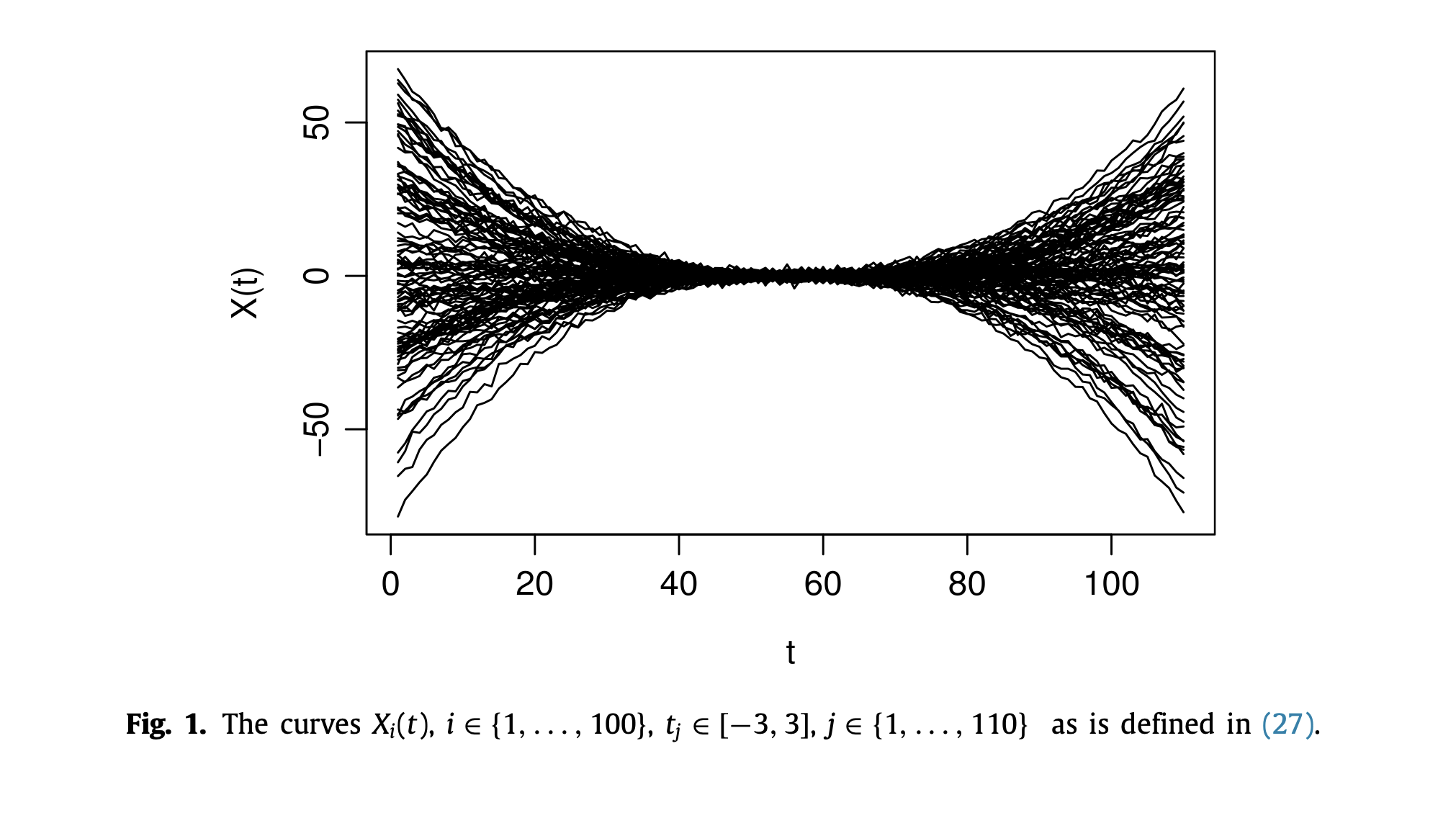
Abstract
The aim of this paper is to nonparametrically estimate the expectile regression in the case of a functional predictor and a scalar response. More precisely, we construct a kernel-type estimator of the expectile regression function. The main contribution of this study is the establishment of the asymptotic properties of the expectile regression estimator. Precisely, we establish the almost complete convergence with rate. Furthermore, we obtain the asymptotic normality of the proposed estimator under some mild conditions. We provide how to apply our results to construct the confidence intervals. The case of functional predictor is of particular interest and challenge, both from theoretical as well as practical point of view. We discuss the potential impacts of functional expectile regression in NFDA with a particular focus on the supervised classification, prediction and financial risk analysis problems. Finally, the finite-sample performances of the model and the estimation method are illustrated using the analysis of simulated data and real data coming from the financial risk analysis.
Asymptotic properties of \(M\)-estimators based on estimating equations and censored data in semi-parametric models with multiple change points.
Journal
Journal of Mathematical Analysis and Applications, 2021
Abstract
Statistical models with multiple change points in presence of censored data are used in many fields; however, the theoretical properties of \(M\)-estimators of such models have received relatively little attention. The main purpose of the present work is to investigate the asymptotic properties of \(M\)-estimators of the parameters of a multiple change-point model for a general class of models in which the form of the distribution can change from segment to segment and in which, possibly, there are parameters that are common to all segments, in the setting of a known number of change points. Consistency of the \(M\)-estimators of the change points is established and the rate of convergence is determined. The asymptotic normality of the \(M\)-estimators of the parameters of the within-segment distributions is established. Since the approaches used in the complete data models are not easily extended to multiple change-point models in the presence of censoring, we have used some general results of Kaplan-Meier integrals. We investigate the performance of the methodology for small samples through a simulation study.
Uniform consistency and uniform in bandwidth consistency for nonparametric regression estimates and conditional \(U\)-statistics involving functional data.
Journal
Journal of Nonparametric Statistics, 2020
Abstract
W. Stute [(1991), Annals of Probability, 19, 812-825] introduced a class of so-called conditional \(U\)-statistics, which may be viewed as a generalisation of the Nadaraya-Watson estimates of a regression function. Stute proved their strong pointwise consistency to \[ m(\mathbf{t}):=\mathbb{E}\left[\varphi\left(Y_1, \ldots, Y_m\right) \mid\left(X_1, \ldots, X_m\right)=\mathbf{t}\right], \quad \text { for } \mathbf{t} \in \mathbb{R}^{d m} . \] We apply the methods developed in Dony and Mason [(2008), Bernoulli, 14(4), 1108-1133] to establish uniformity in \(\mathbf{t}\) and in bandwidth consistency (i.e. \(h_n, h_n \in\left[a_n, b_n\right]\) where \( 0\leq a_n\leq b_n \rightarrow 0\) at some specific rate) to \(m(\mathbf{t})\) of the estimator proposed by Stute when \(Y\) and covariates \(X\) are functional taking value in some abstract spaces. In addition, uniform consistency is also established over \(\varphi \in \mathcal{F}\) for a suitably restricted class \(\mathcal{F}\). The theoretical uniform consistency results, established in this paper, are (or will be) key tools for many further developments in functional data analysis. Applications include the Nadaraya-Watson kernel estimators and the conditional distribution function. Our theorems allow data-driven local bandwidths for these statistics.
Selected recent talks
Coming
- Coming
- University of Technology of Compiègne
Students
Ph.D. :
- Chrisanthi PAPAMICHAIL, Université de Technologie de Compiègne.
Co-encadrement (50%) avec N. Limnios (Université de Technologie de Compiègne). (10/2012 -- 06/2016)
Titre : Estimation des systèmes dynamiques avec applications en mécanique.
Allocation : Ministère de l'Enseignement Supérieur et de la Recherche. - Boutheina NEMOUCHI, Université de Technologie de Compiègne. (10/2016 -- 06/2020)
Titre : Contributions à la théorie des processus empiriques et des $U$-processus conditionnels.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Mustapha MOHAMMEDI, Université Djillali Liabes de Sidi Bel Abbes-Algérie.
Co-encadrement (50%) avec A. Laksaci. (10/2017 -- 02/2021)
Titre : Contribution à l'estimation non paramétrique des expectiles en statistique fonctionnelle.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Thouria El HAJDALI, Université de Constantine-Algérie.
Co-encadrement (90%) avec Prof. Fatiha Messaci. (10/2018 -- 07/2021)
Titre : Sur les problèmes d'estimation non paramétrique.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Anouar Abdeldjaoued FERFACHE, Université de Technologie de Compiègne. (10/2018 -- 12/2021)
Titre : Les M-estimateurs et leurs applications pour les points de rupture.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Han GUO, Université de Technologie de Compiègne.
Co-encadrement (25%) avec N. Limnios, F. Druesne, P. Feissel. (10/2018 -- 02/2022)
Titre : Développement d'un dialogue essai-calcul dans un cadre probabiliste pour la validation de châssis automobile.
Financement : Bourse CIFRE Renault. - Youssouf SOUDDI, Université Dr. Moulay Tahar de Saida-Algérie.
Co-encadrement (70%) avec Prof. Fethi Madani. (10/2018 -- 07/2022)
Titre : Estimation non paramétrique pour les processus empiriques conditionnels avec covariables fonctionnelles.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Inass SOUKARIEH, Université de Technologie de Compiègne. (10/2019 -- 12/2022)
Titre : Theoretical contribution to the U-processes in Markov and dependent setting: Asymptotics and bootstraps.
Allocation : Ministère de l'Enseignement Supérieur et de la Recherche. - Ame NEZZAL, Université de Technologie de Compiègne. (10/2019 -- 10/2022)
Titre : Contributions à la théorie des U-statistiques et processus empiriques.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Soumaya ALLAOUI, Huazhong University of Science and Technology.
Co-encadrement (70%) avec Prof. Xiequan Fan. (10/2018 -- 05/2023)
Titre : Estimation non-paramétrique par ondelettes de la densité et la régression sur données faiblement dépendantes.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Badreddine SLIME, Université de Technologie de Compiègne. (10/2020 -- 10/2023)
Titre : Sur les applications de la VaR conditionnelle.
Validation : des acquis de l'expérience. - Nourelhouda TAACHOUCHE, Université de Technologie de Compiègne. (12/2020 -- 12/2023)
Titre : Contributions théoriques aux U-processus conditionnels dans un cadre abstrait.
Financement : Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Algérien. - Breix Michael AGUA, Université de Technologie de Compiègne. (10/2022 -- 12/2025)
Titre : Single Index Regression for Locally Stationary Processes.
Financement : PhilFrance-DOST. - Jan Nino TINIO, Université de Technologie de Compiègne.
Co-encadrement (50%) avec M. Alaya. (10/2022 -- 12/2025)
Titre : Processus empiriques conditionnels pour les séries temporelles fonctionnelles localement stationnaires.
Financement : PhilFrance-DOST. - Noura OMAR, Université de Technologie de Compiègne.
Co-encadrement (50%) avec M. Alaya. (10/2023 -- 12/2026)
Titre : Régression de Fréchet définie sur des espaces métriques.
Allocation : Ministère de l'Enseignement Supérieur et de la Recherche.
Services
Consulting
Offre d'expertise
Je propose une expertise approfondie dans les domaines suivants :
- Apprentissage automatique (Machine Learning)
- Apprentissage profond (Deep Learning)
- Statistique
- Big Data
- Science des données
- Domaines connexes
N'hésitez pas à me contacter pour échanger autour de projets, collaborations ou toute idée que vous souhaiteriez discuter.
Contact
I am affiliated with the Laboratory of Applied Mathematics (LMAC), within the Department of Computer Science at the University of Technology of Compiègne.
If you have ideas, research questions, or potential collaborations to explore, I would be glad to hear from you.
Tel: (+33) 3 44 23 44 69